Set Theory & Combinatorics
Discrete foundations for data structures, algorithms, and logical reasoning
Set Theory & Combinatorics
Set theory and combinatorics form the discrete mathematical foundation essential for computer science, data structures, algorithm analysis, and probability theory.
What You'll Learn
By the end of this module, you will be able to:
| # | Topic | Skill |
|---|---|---|
| 1 | Sets & Notation | Read and write set notation (∈, ∪, ∩, ⊆) |
| 2 | Venn Diagrams | Visualize Union, Intersection, Difference operations |
| 3 | Cardinality | Calculate set sizes using Inclusion-Exclusion |
| 4 | Power Set | Find all subsets of a set (2^n formula) |
| 5 | Permutations | Count ordered arrangements (n!) |
| 6 | Combinations | Count unordered selections C(n,r) |
| 7 | Relations | Identify Reflexive, Symmetric, Transitive properties |
| 8 | Functions | Count mappings between sets |
| 9 | De Morgan's Laws | Simplify complement expressions |
| 10 | Problem Solving | Apply these concepts to CUET PG style MCQs |
Math Notation & Pronunciation Guide
Set Notation:
- ∈ - pronounced "element of" or "in" - membership (x ∈ A means x is in set A)
- ∉ - pronounced "not element of" - non-membership
- ⊂ - pronounced "subset of" - A ⊂ B means all of A is in B
- ⊆ - pronounced "subset or equal to" - includes equality
- ∪ - pronounced "union" - combines sets
- ∩ - pronounced "intersection" - common elements
- ∅ - pronounced "empty set" or "null set"
- |A| - pronounced "cardinality of A" - number of elements
Combinatorics:
- n! - pronounced "n factorial" - product of 1 to n
- P(n,r) or ⁿPᵣ - pronounced "n permute r" - ordered arrangements
- C(n,r) or ⁿCᵣ or (n choose r) - pronounced "n choose r" - unordered selections
Greek Letters:
- Σ (sigma) - summation
- Π (pi) - product notation
Key Concepts
1. Sets - Fundamental Definitions
What is a Set? A set is an unordered collection of distinct objects (called elements or members).
Common Set Notations:
# Python sets mirror mathematical sets
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}
# Set builder notation (math): {x | x > 0 and x < 10}
# Python equivalent:
C = {x for x in range(1, 10)} # {1, 2, 3, 4, 5, 6, 7, 8, 9}
# Empty set
empty = set() # or ∅ in math notation
Special Sets:
- Natural Numbers (ℕ): {0, 1, 2, 3, ...} or {1, 2, 3, ...}
- Integers (ℤ): {..., -2, -1, 0, 1, 2, ...}
- Rational Numbers (ℚ): All fractions p/q
- Real Numbers (ℝ): All numbers on the number line
- Universal Set (U): Contains all elements under consideration
2. Venn Diagrams - Visual Representation
What is a Venn Diagram? A Venn diagram uses overlapping circles to show relationships between sets visually.
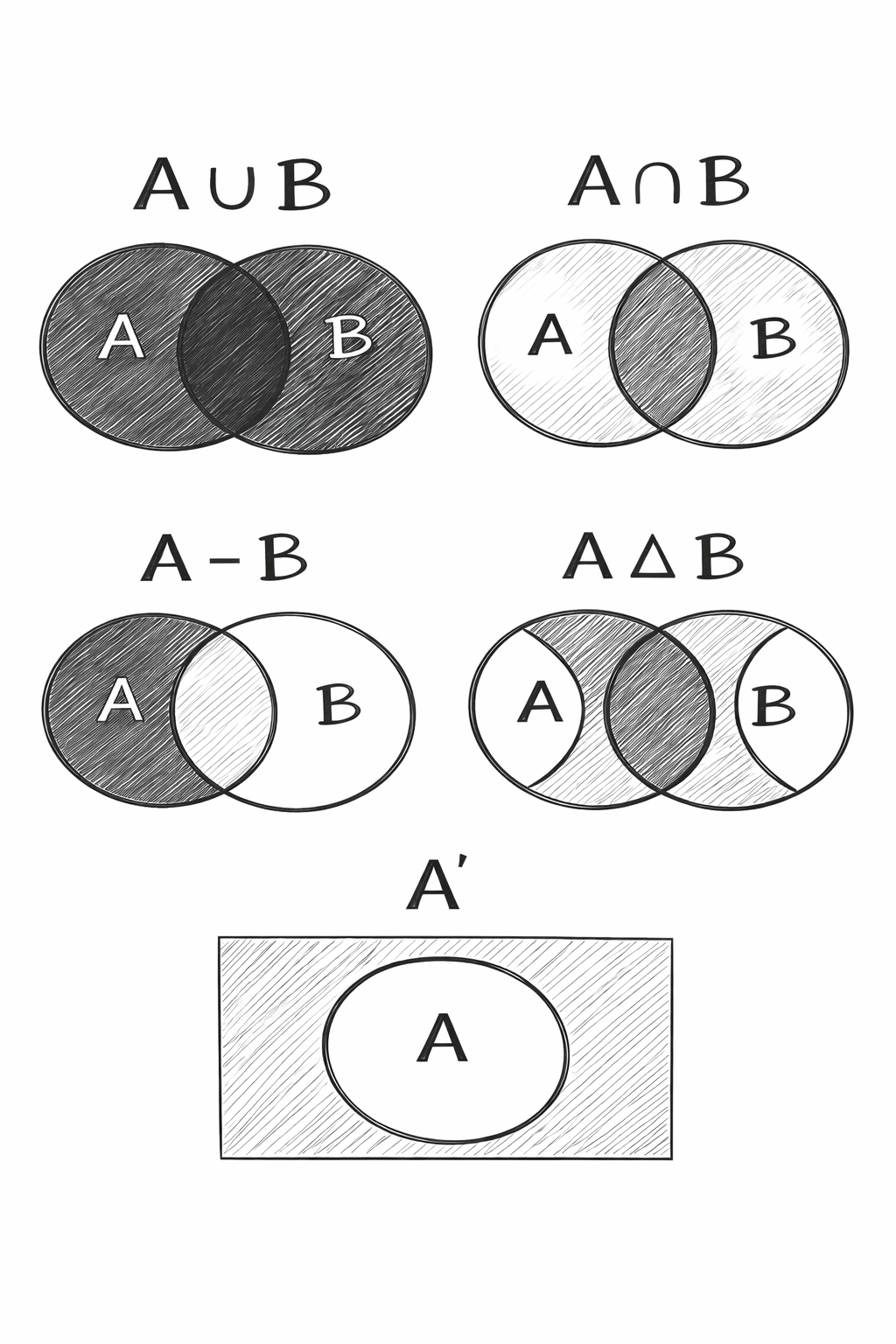
Set Operations Summary:
| Operation | Symbol | Shaded Region | Meaning |
|---|---|---|---|
| Union | A ∪ B | Both circles | Elements in A OR B (or both) |
| Intersection | A ∩ B | Overlap only | Elements in A AND B |
| Difference | A - B | Left crescent | Elements in A but NOT in B |
| Symmetric Diff | A △ B | Both crescents | Elements in A OR B, but NOT both |
| Complement | A' | Outside A | Everything NOT in A |
Practical Problem-Solving with Venn Diagrams:
Problem: In a class of 50 students, 30 play cricket, 25 play football, and 10 play both. Find students who play only cricket, only football, at least one sport, and neither sport.
Step 1: Define the Sets
Let's formally define our sets first:
- U = Universal Set = All 50 students in the class
- C = Set of Cricket players → |C| = 30
- F = Set of Football players → |F| = 25
- C ∩ F = Students who play BOTH → |C ∩ F| = 10
Step 2: Identify the 4 Regions of the Venn Diagram
Think of two overlapping circles (C and F) inside a rectangle (U):
| Region | Description | Count |
|---|---|---|
| Only Cricket | Left circle only (C - F) | 20 |
| Both Sports | Overlap area (C ∩ F) | 10 |
| Only Football | Right circle only (F - C) | 15 |
| Neither | Outside both circles | 5 |
| Total (U) | All students | 50 |
Step 3: Calculate Each Region
Region 1 — Only Cricket (C - F): These students play cricket but NOT football. Formula: |C - F| = |C| - |C ∩ F| = 30 - 10 = 20 students
Why subtract? Because |C| = 30 includes BOTH the "only cricket" AND "both sports" students. Removing the overlap gives us only-cricket.
Region 2 — Only Football (F - C): These students play football but NOT cricket. Formula: |F - C| = |F| - |C ∩ F| = 25 - 10 = 15 students
Region 3 — Both Sports (C ∩ F): Already given: |C ∩ F| = 10 students
Region 4 — At Least One Sport (C ∪ F) — Inclusion-Exclusion: Formula: |C ∪ F| = |C| + |F| - |C ∩ F|
NOTE: Why subtract |C ∩ F|? This is the KEY insight! When you add |C| + |F|, the 10 students who play BOTH sports get counted TWICE — once in cricket's 30, and once in football's 25. Subtracting once removes the double-counting.
|C ∪ F| = 30 + 25 - 10 = 45 students
Region 5 — Neither Sport (C ∪ F)': Students outside both circles = Total - At least one Formula: |(C ∪ F)'| = |U| - |C ∪ F| = 50 - 45 = 5 students
Step 4: Verify (all regions must add up to |U|) Only Cricket + Only Football + Both + Neither = 20 + 15 + 10 + 5 = 50 (verified)
# Step 1: Define known values
total_students = 50 # |U| = Universal Set
cricket = 30 # |C| = Cricket players
football = 25 # |F| = Football players
both = 10 # |C ∩ F| = Play both sports
# Step 2: Apply Inclusion-Exclusion for Union
# |C ∪ F| = |C| + |F| - |C ∩ F|
# WHY subtract? Adding C + F double-counts the 10 students
# who play BOTH. Subtracting removes the duplicate.
either = cricket + football - both
print(f"At least one sport (C ∪ F): {either}") # 45
# Step 3: Find Only Cricket = C - F (set difference)
# |C| includes both "only cricket" AND "both" students
# So: Only Cricket = |C| - |C ∩ F|
only_cricket = cricket - both
print(f"Only cricket (C - F): {only_cricket}") # 20
# Step 4: Find Only Football = F - C (set difference)
only_football = football - both
print(f"Only football (F - C): {only_football}") # 15
# Step 5: Find Neither = Complement of Union
# Students outside both circles = |U| - |C ∪ F|
neither = total_students - either
print(f"Neither sport (C ∪ F)': {neither}") # 5
# Step 6: Verify — all regions must equal total
assert only_cricket + only_football + both + neither == total_students
print(f"Verification: {only_cricket} + {only_football} + {both} + {neither} = {total_students} OK")
MCQ Shortcut: In exams, if they give you "neither", work backwards! |C ∪ F| = Total - Neither, then use |C ∩ F| = |C| + |F| - |C ∪ F|
3. Set Operations
Let A = {1, 2, 3, 4} and B = {3, 4, 5, 6}. We will use these two sets to demonstrate every operation.
Union (A ∪ B) — "OR"
Definition: A ∪ B = {x | x ∈ A or x ∈ B} — collect ALL elements from both sets, no duplicates.
Step-by-step — check each element:
| Element | In A? | In B? | In A ∪ B? (A or B) |
|---|---|---|---|
| 1 | Yes | No | Yes (in A) |
| 2 | Yes | No | Yes (in A) |
| 3 | Yes | Yes | Yes (in both) |
| 4 | Yes | Yes | Yes (in both) |
| 5 | No | Yes | Yes (in B) |
| 6 | No | Yes | Yes (in B) |
Result: A ∪ B = {1, 2, 3, 4, 5, 6}
TIP: Key insight: Elements 3 and 4 appear in BOTH sets, but in the union they appear only ONCE. Sets never have duplicates!
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
# Union: Python uses | operator (or .union() method)
# Math: A ∪ B — collect all unique elements from both
A_union_B = A | B
print(f"A ∪ B = {A_union_B}") # {1, 2, 3, 4, 5, 6}
print(f"|A ∪ B| = {len(A_union_B)}") # 6 (not 8, because 3,4 aren't counted twice)
Intersection (A ∩ B) — "AND"
Definition: A ∩ B = {x | x ∈ A and x ∈ B} — only elements that appear in BOTH sets.
Step-by-step — check each element:
| Element | In A? | In B? | In A ∩ B? (A and B) |
|---|---|---|---|
| 1 | Yes | No | No (not in B) |
| 2 | Yes | No | No (not in B) |
| 3 | Yes | Yes | Yes (in both!) |
| 4 | Yes | Yes | Yes (in both!) |
| 5 | No | Yes | No (not in A) |
| 6 | No | Yes | No (not in A) |
Result: A ∩ B = {3, 4}
TIP: MCQ Trap: If A ∩ B = ∅ (empty set), the sets are called disjoint — they share NO elements.
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
# Intersection: Python uses & operator (or .intersection() method)
# Math: A ∩ B — only elements in BOTH sets
A_intersect_B = A & B
print(f"A ∩ B = {A_intersect_B}") # {3, 4}
print(f"|A ∩ B| = {len(A_intersect_B)}") # 2
# Check if sets are disjoint (no common elements)
C = {7, 8, 9}
print(f"A and C disjoint? {A.isdisjoint(C)}") # True (A ∩ C = ∅)
Difference (A - B) — "In A but NOT in B"
Definition: A - B = {x | x ∈ A and x ∉ B} — remove B's elements from A.
Step-by-step — check each element of A:
| Element of A | Also in B? | In A - B? |
|---|---|---|
| 1 | No | Yes (keep — not in B) |
| 2 | No | Yes (keep — not in B) |
| 3 | Yes | No (remove — it's in B) |
| 4 | Yes | No (remove — it's in B) |
Result: A - B = {1, 2}
NOTE: A - B ≠ B - A! Order matters in set difference! B - A = {5, 6} (elements in B but not in A)
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
# Set Difference: Python uses - operator (or .difference() method)
# Math: A - B — elements in A that are NOT in B
A_minus_B = A - B
B_minus_A = B - A
print(f"A - B = {A_minus_B}") # {1, 2}
print(f"B - A = {B_minus_A}") # {5, 6}
# IMPORTANT: A - B ≠ B - A (set difference is NOT commutative!)
print(f"A - B == B - A? {A_minus_B == B_minus_A}") # False
Complement (A') — "Everything NOT in A"
Definition: A' = U - A = {x | x ∈ U and x ∉ A}
The complement depends on the Universal Set U — the "universe" of all possible elements.
Example: Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and A = {1, 2, 3, 4}
| Element | In U? | In A? | In A'? (in U but not A) |
|---|---|---|---|
| 1 | Yes | Yes | No |
| 2 | Yes | Yes | No |
| 3 | Yes | Yes | No |
| 4 | Yes | Yes | No |
| 5 | Yes | No | Yes |
| 6 | Yes | No | Yes |
| 7-10 | Yes | No | Yes |
Result: A' = {5, 6, 7, 8, 9, 10}
TIP: Important Properties:
- A ∪ A' = U (a set and its complement cover everything)
- A ∩ A' = ∅ (a set and its complement share nothing)
- (A')' = A (double complement gives back the original)
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} # Universal set
A = {1, 2, 3, 4}
# Complement: A' = U - A (everything in universe NOT in A)
A_complement = U - A
print(f"A' = {A_complement}") # {5, 6, 7, 8, 9, 10}
# Verify properties
print(f"A ∪ A' = U? {(A | A_complement) == U}") # True
print(f"A ∩ A' = ∅? {len(A & A_complement) == 0}") # True
Symmetric Difference (A △ B) — "In one OR the other, but NOT both"
Definition: A △ B = (A ∪ B) - (A ∩ B) = (A - B) ∪ (B - A)
This gives you elements that are in EXACTLY ONE of the two sets.
Step-by-step:
| Element | In A? | In B? | In exactly one? | In A △ B? |
|---|---|---|---|---|
| 1 | Yes | No | Yes (only A) | Yes |
| 2 | Yes | No | Yes (only A) | Yes |
| 3 | Yes | Yes | No (in both!) | No |
| 4 | Yes | Yes | No (in both!) | No |
| 5 | No | Yes | Yes (only B) | Yes |
| 6 | No | Yes | Yes (only B) | Yes |
Result: A △ B = {1, 2, 5, 6}
TIP: Two equivalent ways to calculate:
- Method 1: (A ∪ B) - (A ∩ B) = {1,2,3,4,5,6} - {3,4} = {1,2,5,6}
- Method 2: (A - B) ∪ (B - A) = {1,2} ∪ {5,6} = {1,2,5,6}
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
# Symmetric Difference: Python uses ^ operator
# Math: A △ B — elements in EXACTLY ONE set
symmetric = A ^ B
print(f"A △ B = {symmetric}") # {1, 2, 5, 6}
# Verify both methods give same result
method1 = (A | B) - (A & B) # Union minus Intersection
method2 = (A - B) | (B - A) # Only-A plus Only-B
print(f"Method 1 (A∪B)-(A∩B) = {method1}") # {1, 2, 5, 6}
print(f"Method 2 (A-B)∪(B-A) = {method2}") # {1, 2, 5, 6}
print(f"All methods equal? {symmetric == method1 == method2}") # True
3. Cardinality
Cardinality = how many elements are in the set. Written as |A|.
Basic Examples:
| Set | Elements | |Set| (Cardinality) | |:----|:---------|:--------------------| | A = {1, 2, 3, 4, 5} | 1, 2, 3, 4, 5 | |A| = 5 | | B = {a, b} | a, b | |B| = 2 | | ∅ (empty set) | (nothing) | |∅| = 0 | | {∅} | ∅ itself | |{∅}| = 1 (the empty set IS an element!) |
NOTE: MCQ Trap: |{∅}| = 1, NOT 0! The set contains one element (which happens to be the empty set).
A = {1, 2, 3, 4, 5}
print(f"|A| = {len(A)}") # 5
# Empty set cardinality
empty = set()
print(f"|∅| = {len(empty)}") # 0
# CAUTION: {∅} has 1 element (the empty set itself)
# In Python, we can't directly nest sets, but conceptually:
# |{∅}| = 1, NOT 0!
Cardinality of Union — Inclusion-Exclusion Principle:
This is the MOST IMPORTANT formula for MCQs. It tells us how many elements are in a union.
For 2 sets: |A ∪ B| = |A| + |B| - |A ∩ B|
For 3 sets (extended formula): |A ∪ B ∪ C| = |A| + |B| + |C| - |A ∩ B| - |A ∩ C| - |B ∩ C| + |A ∩ B ∩ C|
TIP: Why does this work?
- Adding all three counts elements in multiple sets MORE THAN ONCE
- Subtracting pairwise intersections corrects the over-counting
- But elements in ALL THREE sets get subtracted too many times, so add them back
Worked Example: In a survey of 100 students:
- 40 like Math, 35 like Science, 30 like English
- 15 like Math & Science, 10 like Math & English, 12 like Science & English
- 5 like all three
|M ∪ S ∪ E| = 40 + 35 + 30 - 15 - 10 - 12 + 5 = 73 students like at least one subject Students who like NONE = 100 - 73 = 27 students
# Two-set Inclusion-Exclusion
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
# Why subtract? Because |A| + |B| = 4 + 4 = 8, but elements
# 3 and 4 are counted TWICE. Subtracting |A ∩ B| = 2 fixes this.
union_size = len(A | B) # Actual: 6
calculated = len(A) + len(B) - len(A & B) # 4 + 4 - 2 = 6
print(f"|A ∪ B| = {union_size}") # 6
print(f"|A| + |B| - |A ∩ B| = {calculated}") # 6 (verified)
# Three-set Inclusion-Exclusion
math_students = 40
science_students = 35
english_students = 30
math_science = 15
math_english = 10
science_english = 12
all_three = 5
at_least_one = (math_students + science_students + english_students
- math_science - math_english - science_english
+ all_three)
print(f"Like at least one subject: {at_least_one}") # 73
print(f"Like none: {100 - at_least_one}") # 27
4. Power Set
The power set P(A) is the set of ALL possible subsets of A, including ∅ and A itself.
Formula: If |A| = n, then |P(A)| = 2ⁿ
TIP: Why 2ⁿ? Each element has exactly 2 choices: either it's IN the subset or NOT. So for n elements, there are 2 × 2 × ... × 2 (n times) = 2ⁿ possible subsets.
Example: Let A = {1, 2, 3}. List ALL subsets:
| Element 1 | Element 2 | Element 3 | Subset |
|---|---|---|---|
| No | No | No | {} (empty set ∅) |
| Yes | No | No | {1} |
| No | Yes | No | {2} |
| No | No | Yes | {3} |
| Yes | Yes | No | {1, 2} |
| Yes | No | Yes | {1, 3} |
| No | Yes | Yes | {2, 3} |
| Yes | Yes | Yes | {1, 2, 3} |
Total = 2³ = 8 subsets
P(A) = {∅, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}
NOTE: MCQ Traps:
- P(A) ALWAYS includes ∅ (the empty set is a subset of every set)
- P(A) ALWAYS includes A itself
- P(∅) = {∅}, so |P(∅)| = 2⁰ = 1 (not 0!)
from itertools import chain, combinations
def power_set(s):
"""Generate all subsets of a set"""
s = list(s)
return list(chain.from_iterable(
combinations(s, r) for r in range(len(s) + 1)
))
A = {1, 2, 3}
P_A = power_set(A)
print(f"Power set of {A}:")
for subset in P_A:
print(f" {set(subset) if subset else '∅'}")
# Verify the formula: |P(A)| = 2^|A|
print(f"|P(A)| = {len(P_A)}") # 8
print(f"2^|A| = 2^{len(A)} = {2**len(A)}") # 8 (verified)
# Quick exam calculations:
# |A| = 0 → |P(A)| = 1
# |A| = 3 → |P(A)| = 8
# |A| = 5 → |P(A)| = 32
# |A| = 10 → |P(A)| = 1024
5. Permutations
Permutation = an ORDERED arrangement. The KEY word is order matters.
Formula: P(n, r) = n! / (n-r)!
Where n = total items, r = items to arrange, and n! = n × (n-1) × (n-2) × ... × 1
TIP: Think of it as filling slots: You have r empty slots to fill from n items.
Example: How many 3-letter codes from {A, B, C, D, E}? (n=5, r=3)
| Slot | Choices Left | Why? |
|---|---|---|
| 1st letter | 5 choices | All 5 letters available |
| 2nd letter | 4 choices | 1 letter already used |
| 3rd letter | 3 choices | 2 letters already used |
Total = 5 × 4 × 3 = 60 arrangements
Using the formula: P(5,3) = 5! / (5-3)! = 120 / 2 = 60 (verified)
NOTE: ABC ≠ BAC ≠ CAB — these are THREE different permutations because order matters!
Common MCQ patterns:
- "How many ways to ARRANGE" → Permutation
- "How many PASSWORDS of length r" → Permutation
- "How many ways can n people LINE UP" → n! (special case: P(n,n))
- "RANKINGS / positions" → Permutation
import math
from itertools import permutations
# Factorial: n! = n × (n-1) × ... × 1
print(f"5! = 5×4×3×2×1 = {math.factorial(5)}") # 120
print(f"0! = {math.factorial(0)}") # 1 (by definition!)
# Permutation formula: P(n, r) = n! / (n-r)!
def P(n, r):
return math.factorial(n) // math.factorial(n - r)
# 3-letter codes from 5 letters
n, r = 5, 3
print(f"P({n},{r}) = {n}!/({n}-{r})! = {math.factorial(n)}/{math.factorial(n-r)} = {P(n,r)}") # 60
# Special case: arrange ALL items → P(n,n) = n!
people = 4
print(f"4 people in a line: P(4,4) = 4! = {P(people, people)}") # 24
Exam Shortcut: For "arrange r from n", just multiply: n × (n-1) × ... down to r numbers. P(5,3) = 5 × 4 × 3 = 60. No need to compute full factorials!
6. Combinations
Combination = an UNORDERED selection. The KEY word is order doesn't matter.
Formula: C(n, r) = n! / (r! × (n-r)!)
Also written as "n choose r" or ⁿCᵣ
TIP: Why divide by r!? Because a permutation counts ABC, BAC, CAB as 3 different results. But in a combination, they're all the SAME team {A, B, C}. So we divide by r! to remove the duplicate orderings.
Example: Select 3 team members from {Alice, Bob, Charlie, Dave, Eve}. (n=5, r=3)
Step 1: Permutations = P(5,3) = 60 (ordered arrangements) Step 2: Each group of 3 people can be ordered in r! = 3! = 6 ways Step 3: Combinations = 60 / 6 = 10 unique teams
The 10 teams are:
| # | Team | Note |
|---|---|---|
| 1 | {Alice, Bob, Charlie} | ABC = BAC = CAB (all same team) |
| 2 | {Alice, Bob, Dave} | |
| 3 | {Alice, Bob, Eve} | |
| 4 | {Alice, Charlie, Dave} | |
| 5 | {Alice, Charlie, Eve} | |
| 6 | {Alice, Dave, Eve} | |
| 7 | {Bob, Charlie, Dave} | |
| 8 | {Bob, Charlie, Eve} | |
| 9 | {Bob, Dave, Eve} | |
| 10 | {Charlie, Dave, Eve} |
Common MCQ patterns:
- "How many ways to SELECT / CHOOSE" → Combination
- "How many COMMITTEES / TEAMS" → Combination
- "How many HANDSHAKES in a group" → C(n, 2)
- "How many SUBSETS of size r" → C(n, r)
import math
from itertools import combinations
# Combination formula: C(n,r) = n! / (r! × (n-r)!)
def C(n, r):
return math.factorial(n) // (math.factorial(r) * math.factorial(n - r))
# Or use Python's built-in (cleaner)
print(f"C(5, 3) = {math.comb(5, 3)}") # 10
# List all combinations to see they're unordered
candidates = ['Alice', 'Bob', 'Charlie', 'Dave', 'Eve']
teams = list(combinations(candidates, 3))
print(f"All {len(teams)} possible teams:")
for i, team in enumerate(teams, 1):
print(f" Team {i}: {team}")
Permutation vs Combination — The Ultimate Comparison:
| Permutation P(n,r) | Combination C(n,r) | |
|---|---|---|
| Order | Matters (ABC ≠ BAC) | Doesn't matter (ABC = BAC) |
| Formula | n!/(n-r)! | n!/(r!(n-r)!) |
| Keywords | arrange, line up, rank, password | select, choose, committee, team |
| P(5,3) | 60 | 10 |
| Always | P(n,r) ≥ C(n,r) | C(n,r) ≤ P(n,r) |
Relationship: P(n, r) = C(n, r) × r!
TIP: Why? Permutations = (number of groups) × (ways to arrange each group) 60 = 10 × 6. Each of the 10 teams can be arranged in 3! = 6 ways.
# Verify: P(n,r) = C(n,r) × r!
n, r = 5, 3
P_nr = P(n, r) # 60 (ordered arrangements)
C_nr = C(n, r) # 10 (unordered selections)
r_fact = math.factorial(r) # 3! = 6
print(f"P({n},{r}) = C({n},{r}) × {r}!")
print(f"{P_nr} = {C_nr} × {r_fact} = {C_nr * r_fact}") # 60 = 10 × 6 (verified)
7. Pascal's Triangle & Properties
Pascal's Triangle is a visual arrangement where each number equals C(n, r).
The Triangle with actual values:
Row 0: 1 -- C(0,0)
Row 1: 1 1 -- C(1,0) C(1,1)
Row 2: 1 2 1 -- C(2,0) C(2,1) C(2,2)
Row 3: 1 3 3 1 -- C(3,0) C(3,1) C(3,2) C(3,3)
Row 4: 1 4 6 4 1 -- C(4,0) ... C(4,4)
Row 5: 1 5 10 10 5 1 -- C(5,0) ... C(5,5)
TIP: How to build it: Each number = sum of the two numbers directly above it. Example: 6 = 3 + 3, 10 = 4 + 6, 10 = 6 + 4
3 Key Properties (MCQ favorites):
| Property | Formula | Example |
|---|---|---|
| Edges are always 1 | C(n, 0) = C(n, n) = 1 | C(5,0) = C(5,5) = 1 |
| Symmetry | C(n, r) = C(n, n-r) | C(5,2) = C(5,3) = 10 |
| Pascal's Identity | C(n,r) = C(n-1,r-1) + C(n-1,r) | C(4,2) = C(3,1) + C(3,2) = 3+3 = 6 |
TIP: Row Sum: Each row sums to 2ⁿ. Row 3: 1+3+3+1 = 8 = 2³ This makes sense because the total subsets of an n-element set = 2ⁿ!
Exam Shortcuts using Pascal's Triangle:
- Need C(4,2)? Go to Row 4, position 2 → 6
- Need C(5,3)? Row 5, position 3 → 10
- Don't want to calculate? Use symmetry: C(10,8) = C(10,2) = 45 (much easier!)
import math
def pascals_triangle(rows):
"""Generate Pascal's triangle — each entry is C(n, r)"""
triangle = []
for n in range(rows):
row = [math.comb(n, r) for r in range(n + 1)]
triangle.append(row)
return triangle
# Display the triangle
for i, row in enumerate(pascals_triangle(6)):
padding = " " * (5 - i)
values = " ".join(str(x).center(4) for x in row)
print(f"Row {i}: {padding}{values}")
# Verify properties:
print(f"
Property 1: C(5,0) = C(5,5) = {math.comb(5,0)}") # 1
print(f"Property 2: C(5,2) = C(5,3) = {math.comb(5,2)}") # 10 (symmetry)
print(f"Property 3: C(4,2) = C(3,1) + C(3,2) = {math.comb(3,1)} + {math.comb(3,2)} = {math.comb(4,2)}") # 6
print(f"Row 5 sum: {sum(math.comb(5, r) for r in range(6))} = 2^5 = {2**5}") # 32
8. Applications in Computer Science
Set theory and combinatorics appear EVERYWHERE in CS. Here are the top connections:
1. Algorithm Analysis — Why O(2ⁿ) is Bad:
The brute-force approach to many problems involves checking ALL subsets → 2ⁿ possibilities.
| n (items) | 2ⁿ (subsets) | Time at 1M ops/sec |
|---|---|---|
| 10 | 1,024 | < 1ms |
| 20 | 1,048,576 | ~1 second |
| 30 | 1,073,741,824 | ~18 minutes |
| 50 | ~10¹⁵ | ~31 years! |
This is WHY we need dynamic programming and greedy algorithms — to avoid 2ⁿ brute force!
# Power set → brute force subset sum
items = [1, 2, 3, 4, 5]
n = len(items)
total_subsets = 2 ** n # Each item: include or exclude
print(f"n={n} items → {total_subsets} subsets to check")
print(f"n=20 items → {2**20:,} subsets") # Over 1 million!
print(f"n=30 items → {2**30:,} subsets") # Over 1 billion!
2. Database Queries — SQL uses Set Operations!
| SQL Operation | Set Operation | Symbol |
|---|---|---|
| UNION | A ∪ B | Merge results |
| INTERSECT | A ∩ B | Common results |
| EXCEPT | A - B | Rows in A not in B |
| INNER JOIN | A ∩ B (conceptually) | Matching rows |
# SQL-like operations using Python sets
users_usa = {'u1', 'u2', 'u3'} # WHERE country = 'USA'
premium_users = {'u2', 'u3', 'u4'} # WHERE plan = 'premium'
# INTERSECT: USA users who are premium
usa_premium = users_usa & premium_users
print(f"SELECT * FROM users WHERE country='USA' INTERSECT premium")
print(f"Result: {usa_premium}") # {'u2', 'u3'}
# UNION: All users from either group
all_users = users_usa | premium_users
print(f"SELECT * FROM usa_users UNION premium_users")
print(f"Result: {all_users}") # {'u1', 'u2', 'u3', 'u4'}
# EXCEPT: USA users who are NOT premium
usa_free = users_usa - premium_users
print(f"SELECT * FROM usa_users EXCEPT premium_users")
print(f"Result: {usa_free}") # {'u1'}
3. Probability — Combinations in Action:
Probability = (favorable outcomes) / (total outcomes)
Combinations help count both!
Example: Probability of exactly 3 heads in 5 coin flips:
- Step 1: How many ways to choose WHICH 3 flips are heads? → C(5,3) = 10
- Step 2: Total possible outcomes = 2⁵ = 32
- Step 3: P = 10/32 = 0.3125 (31.25%)
import math
# P(exactly k heads in n flips)
n_flips = 5
k_heads = 3
# Step 1: Choose which flips are heads
favorable = math.comb(n_flips, k_heads) # C(5,3) = 10
# Step 2: Total outcomes
total = 2 ** n_flips # 32
# Step 3: Probability
probability = favorable / total
print(f"Ways to get exactly {k_heads} heads: C({n_flips},{k_heads}) = {favorable}")
print(f"Total outcomes: 2^{n_flips} = {total}")
print(f"P({k_heads} heads in {n_flips} flips) = {favorable}/{total} = {probability:.4f}")
TL;DR - Quick Recall
| Concept | Formula/Key Point |
|---|---|
| Union (∪) | A ∪ B = elements in A OR B |
| Intersection (∩) | A ∩ B = elements in A AND B |
| Difference (-) | A - B = elements in A but not B |
| Symmetric Diff (△) | A △ B = (A ∪ B) - (A ∩ B) |
| Complement | A' = U - A |
| De Morgan's 1 | (A ∪ B)' = A' ∩ B' |
| De Morgan's 2 | (A ∩ B)' = A' ∪ B' |
| Cardinality | n(A) = number of elements in A |
| Inclusion-Exclusion | n(A ∪ B) = n(A) + n(B) - n(A ∩ B) |
| Power Set | Size of P(A) = 2^n |
| Factorial | n! = n × (n-1) × ... × 1 |
| Permutation | P(n,r) = n!/(n-r)! — order matters |
| Combination | C(n,r) = n!/(r!(n-r)!) — order doesn't matter |
| P vs C | P(n,r) = C(n,r) × r! |
| Cartesian Product | n(A × B) = n(A) × n(B) |
| Functions A→B | Total = n(B)^n(A) |
| Reflexive | (a,a) ∈ R for all a ∈ A |
| Symmetric | (a,b) ∈ R → (b,a) ∈ R |
| Transitive | (a,b),(b,c) ∈ R → (a,c) ∈ R |
Python Set Operations:
A | B # Union
A & B # Intersection
A - B # Difference
A ^ B # Symmetric difference
len(A) # Cardinality
Additional Resources
Interactive:
Books:
- "Discrete Mathematics and Its Applications" by Kenneth Rosen
- "Concrete Mathematics" by Graham, Knuth, Patashnik
Videos:
Test your understanding
Practice Quiz
10 questions · 90s per question
Each question has a 90-second time limit. Unanswered questions will be auto-submitted when time runs out.